Rotary Positional Embeddings with Relative distances (RoPER)
by Georges Harik and Varuna Jayasiri
Rotary Positional Embeddings (RoPE) (Su et al., 2021) use relative positions in attention score calculation. However, in RoPE, no positional information (relative or otherwise) is added to embeddings.
We investigate adding relative positions of the tokens it pays attention to, to the values of the attention calculation. We call this method RoPER. We evaluate the method and compare it with RoPE in a couple of algorithmic tasks and show that RoPER performs better. We also try it on a language model and show that RoPER doesn’t degrade performance compared to RoPE.
Background
RoPE rotates pairs of features in a 2D plane, by an angle that is a multiple of their position in the modeled sequence. When such a pair participates in dot-product attention only the relative positional difference between that pair and the other pair of embeddings affects the result.
RoPE has shown to be successful in language modeling and is widely being used (Chowdhery et al., 2022).
It has also been shown that auto-regressive transformers can implicitly acquire positional information (Haviv et al., 2022).
Method
RoPER, in addition to using relative positions in the attention score calculation, adds relative positional information explicitly to value embeddings. Specifically, it incorporates the relative positions of the tokens paid attention to.
RoPER rotates the values in attention in a similar way to how RoPE rotates keys and queries. Then, after taking the weighted sum of the values, RoPER rotates the final result in the opposite direction, which leaves the relative positional differences between the current query sequence position and sequence positions of the values, in the final result of the attention.
Relative distances in embeddings
For any head, let be the attention from query position to value position , and be the value embeddings at position . Let's denote individual features as .
Normally, we would take the weighted sum of value embeddings
This doesn't explicitly add any distance information about the positions to final result .
RoPER transforms the value embeddings with and then transformers the weighted sum with but in opposite direction.
For a pair and it transforms with , and then it rotates the weighted sum in the the reverse direction with .
Note that,
Therefore, final output after with the transformations is,
That is, the weighted average of values rotated relative to current position.
Analysis
We compare RoPER with RoPE on three algorithmic tasks. We also show that RoPER performs similar to RoPE on language modeling with a small 200 million parameter transformer.
For the Arithmetic Addition and the Substring by Index tasks, we use a 20 million parameter model (512 embedding size, 6 layers, 8 heads, post layer norm). We sequence of length 641 for training and a batch size of 32. For both these tasks, we report the accuracy of solving the problem after 5,000 training steps. We test the number of correct solutions with random sampling for 128 problems.
For the Substring by Search task, we use a 0.6 million parameter model (128 embedding size, 3 layers, 4 heads, pre-layer norm). We train of sequences of length 513 with a batch size of 16. and we report the final loss after 65,000 steps.
We used a character level tokenizer for all three tasks. We ran 10 training sessions with both methods and reported the mean of the 9 tasks after removing the worst session.
Arithmetic Addition
In this task we test the model’s capacity to solve step-by-step arithmetic addition.
Problem format:
?d=[number1]+[number2]; [steps] d==[final result]#We concatenate multiple problems in the same sequence. We use up to 8 digit numbers for this problem.
Here’s an example:
?d=77+38446365; 7e0+5e0+0e0==12e0 and 7e1+6e1+1e1==14e1 and 0e2+3e2+1e2==4e2 and
0e3+6e3+0e3==6e3 and 0e4+4e4+0e4==4e4 and 0e5+4e5+0e5==4e5 and 0e6+8e6+0e6==8e6 and
0e7+3e7+0e7==3e7 and d==38446442#?d=66623+401; 3e0+1e0+0e0==4e0 and 2e1+0e1+0e1==2e1 and
6e2+4e2+0e2==10e2 and 6e3+0e3+1e3==7e3 and 6e4+0e4+0e4==6e4 and d==67024#?d=25481082+3301219;
...Substring by index
In this problem the model has to retrieve a suffix of a string.
Problem Format:
?s='[string]'; s[[index]:]=='[suffix]'#We concatenate multiple problems in the same sequence. We use upto 8 digits number for this problem.
Example:
?s='dyjeofuxvejmg'; s[8:]=='vejmg'#?s='syoktpufifxes'; ...Substring by Prefix
In this problem the model has to retrieve (complete) fixed length substrings by searching them.
Problem Format:
[random_string]>[substring][random_string]>[substring][random_string]...We randomly select a substring of the current sequence (except >
tokens), and append it to the sequence, followed by a random string string. This is repeated until the total length is equal to the sequence length.
To make the task harder we only use a small vocabulary of size 4.
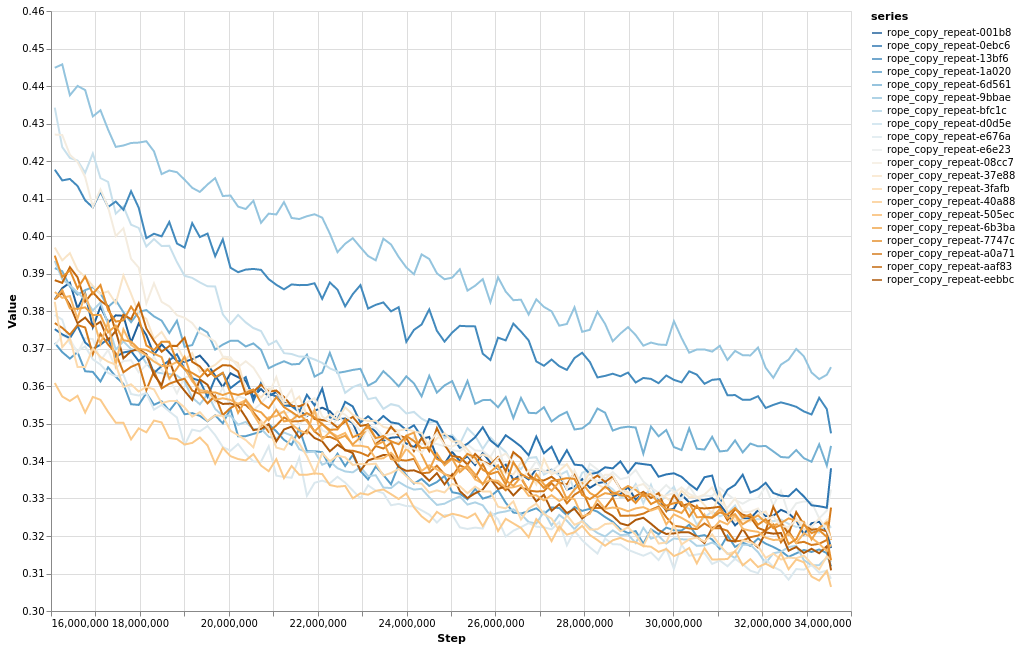
This chart shows the final half of loss curves of the individual training sessions with RoPE and RoPER.
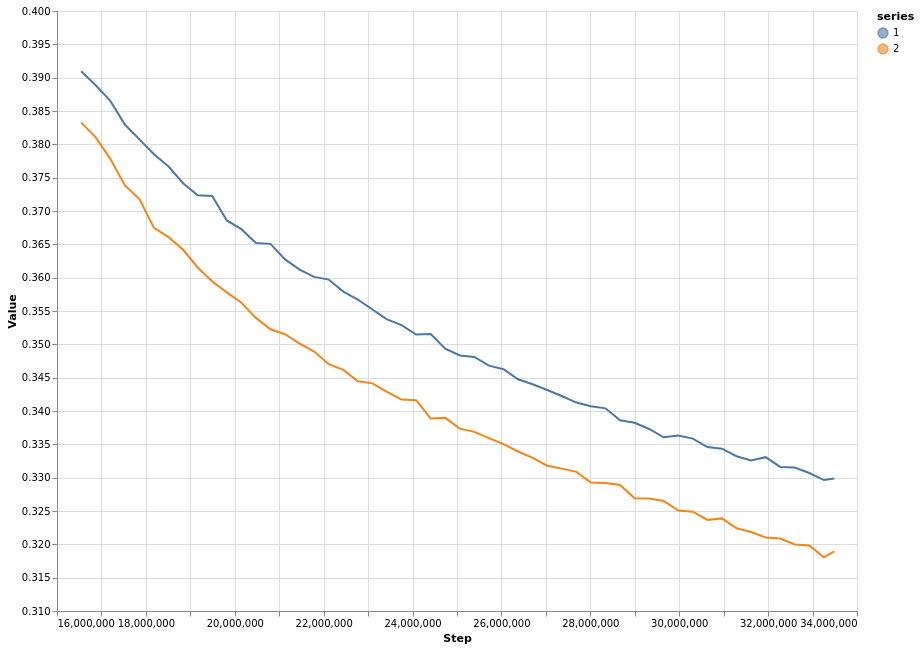
This chart shows the final half of mean loss curves with both methods
Language modeling
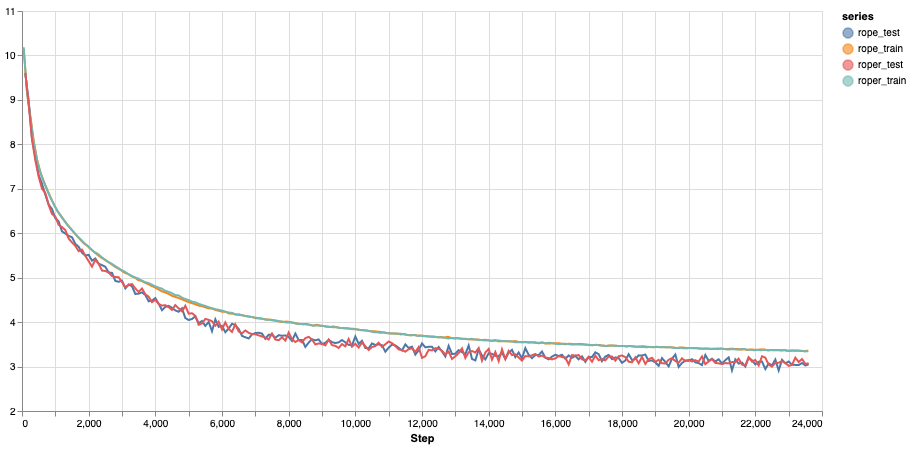
This is the training and validation losses of a 200 million parameter langauge model trained on English Wikipedia dataset. We used sentence piece tokenizer with a vocabulary size of 32,000.
Both runs show similar losses and we can see that RoPER doesn't hurt language modelling capabilities.
Citing this blog post
@misc{harik2022roper,
author = {Georges Harik, Varuna Jayasiri},
title = {Rotary Positional Embeddings with Relative distances},
url = {http://research.labml.ai/RoPER.html},
year = {2022}
}